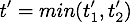La physique

Hypothèses de la simulation

Afin de bien situer le cadre de la simulation, il faut expliquer l'environnement physique de l'expérience :
- On se place dans un cube de côté d'unité unité .
- Chaque particule est modélisée par une sphère de rayon et de masse 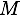qui a une position Position 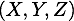et une vitesse vitesse 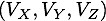initiale.
- On suppose que seules les trois loi de newton (Principe de inertie, Principe fondamentale de la dynamique et Principe des actions réciproques) sont valables. Les forces de frotement et d'interraction (gravité et électromagnétique) ne sont donc pas prises en compte.

Théorie de la physique sur les Chocs

On prend deux particules 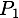et qui entrent en collision entre deux instant (avant la collision) et (après la collision)

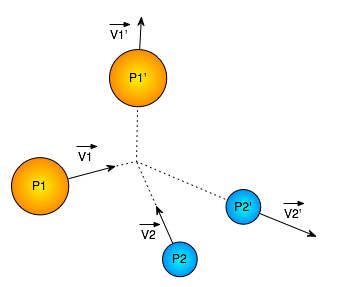
Lors d'une collision entre deux particules, des lois énergétiques doivent être vérifiées afin de satisfaire le modèle de la simulation :
- La loi de la conservation de la quantité de mouvement
La quantité de mouvement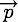 des deux particules est définie par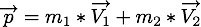

Par la loi de la conservation de la quantité de mouvement, on a :

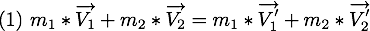
• La loi de la conservation de l'energie
  L'energie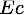 des deux particules est définie par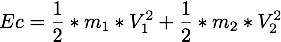

Par la loi de la conservation de l'énergie, on a :

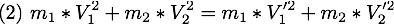
Calcul des nouvelles vitesses après un choc

Dans ce paragraphe, nous allons calculer les nouveaux vecteurs vitesses après une collision.
Définitions et contexte

On note :
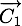- le vecteur position, 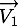le vecteur vitesse avant la collision et 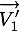le vecteur vitesse après la collision de la particule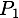
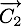- le vecteur position, 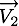le vecteur vitesse avant la collision et 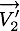le vecteur vitesse après la collision de la particule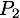
On considère alors le schéma suivant à l'instant précis où deux particules rentrent en collision.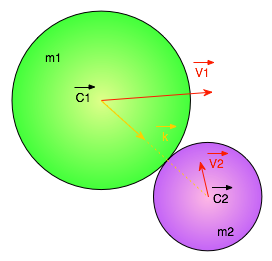

On pose 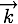, un vecteur unitaire de direction .

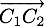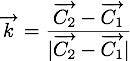
Calculs théorique d'une collision entre deux particules et

On peut réécrire les équations énergétique 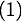et 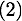qui deviennent

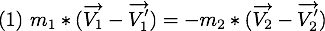
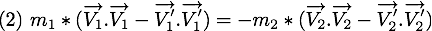
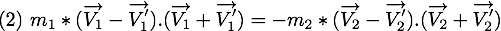
Dans une collision, la quantité de mouvement pour chaque particule est dans la direction du vecteur au moment du contact. La quantité de mouvement est alors donnée par

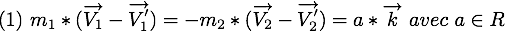
On peut alors réécrire l'équation de conservation de l'énergie

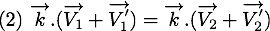
Or nous savons que par 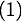, nous avons

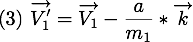
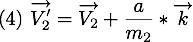
En remplacan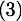t et 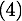dans l'équation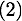, on obtient

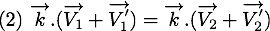
Or, comme , 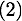devient

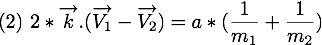
Ainsi, nous connaissons maintenant la valeur de 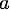qui est

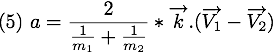
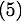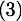En remplacant dans et 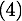, nous pouvons donc connaître les vitesses des deux particules après la collision qui sont

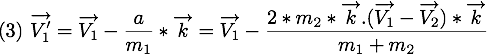
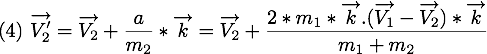
Calculs théorique d'une collision entre une particule 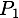et un plan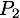

Nous n'allons pas refaire tous les calculs, mais nous servir des vitesses 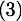et 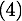trouvées.
Dans le cas présent, nous avons une particule 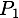de vecteur vitesse 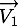avant la collision et le vecteur vitesse 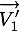après la collision. Pour modéliser le plan 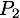, nous considérons qu'il a un vecteur vitesse vecteur 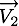et une masse 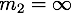. On peut aussi considérer que 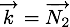, où 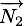est le vecteur normal au plan 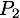. Par passage à la limite sur 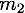, on a

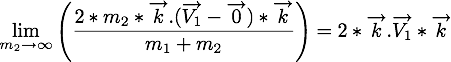
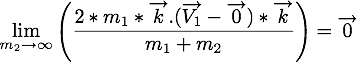
Nous pouvons donc connaître les vitesses de la particule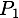 et du plan 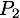après la collision qui sont

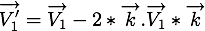
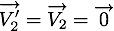
Recherche de l'instant du choc

Définition de l'instant t' de collision

Avant de calculer des vitesses après une collision, nous devons d'abord trouver l'instant 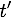qui va produire une collision. Pour cela, nous recherchons le premier instant de collision 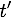qui aura lieu avant toutes les autres collisions

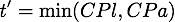
avec

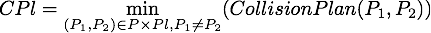
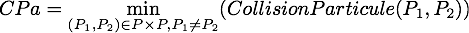
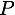est l'ensemble des particules
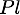est l'ensemble des plans (les 6 facettes du cube)

Nous allons par la suite indiquer comment on calcule
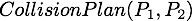et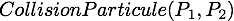

Instant t' de collision entre une particule 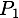et un plan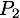

Nous allons expliquer comment la fonction 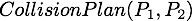calcule l'instant 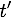de collision entre une particule 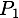et un plan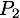

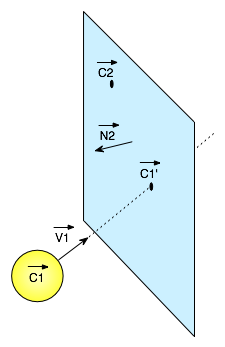
La position de la particule 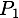à l'instant 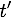de collision est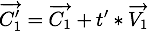
L'équation du plan 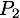est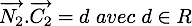

Si la particule 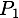intersectionne le pla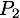n en 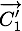, alors, 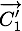doit satisfaire l'équation du plan

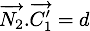
ce qui donne

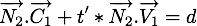
On trouve alors la valeur exacte de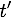

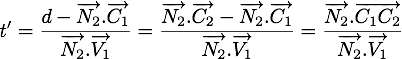
Notez que la fonction 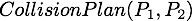ne calcule pas la valeur de 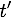si 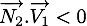(le cas où la particule ne se dirige pas en direction du plan). On aura toujours 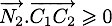car les 6 facettes du cube ont leur normale orienté vers l'intérieur du cube.

Instant t' de collision entre deux particules 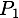et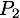

Nous allons expliquer comment la fonction 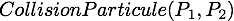calcule l'instant 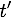de collision entre deux particules 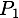et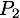

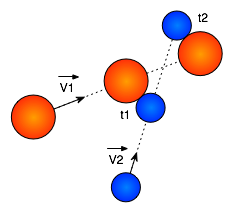
La position de la particule 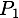à un instant 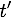ultérieur est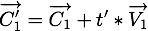

La position de la particule à un instant 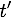ultérieur est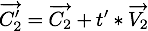

Pour calculer l'instant 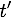de collision, il faut résoudre l'équation

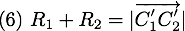
Afin d'écrire le plus simplement possible les calculs qui vont suivre, on pose

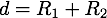
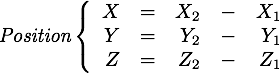
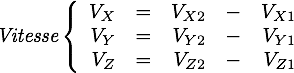
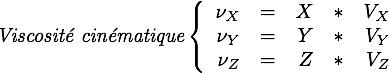
L'équation 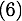devient

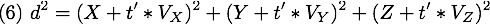
Il faut isoler la variable . Pour cela, on utilise un programme tel que Maple qui va résoudre l'équation. On obtient alors deux solutions de la forme

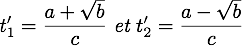
avec

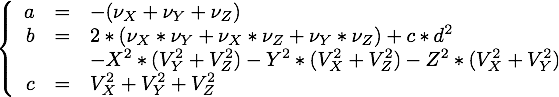
La fonction 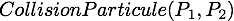ne met pas à jour la valeur de 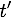si 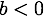(le cas où les particules ne se choquent pas) ou si 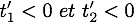(le cas où l'on a bien une collision, mais à un instant t prime inférieur strict à 0). Dans le cas contraire, la fonction 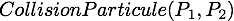met a jour 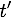et